刷题记录

本文最后更新于：2022年2月6日 晚上

为了避免将来连笔试都过不了，zyk决定每天刷题！

前言

不知不觉，已经好久没有刷题了，算法又太重要了，好焦虑。

学校的OJ只能用c++，但是我准备的又是java，长期不写java，连基本的API都快忘记了，所以写这个帖子，每天刷几道题吧，数量不限，看时间是否充足。

当前目标：先把剑指OFFER刷一遍。

2022-2-6

都是回溯相关问题。解题方式都差不多，树形寻找，递归纵向找每一种方案，for循环横向寻找树形每一层的多种方案。

lc-131.分割回文字符串

lc-93.复原IP地址

lc-78.子集

lc-90.子集2

lc-491.递增子集

2022-2-2

lc-77.组合

mid，递归回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    List<List<Integer>> ans = new LinkedList<List<Integer>>();
    LinkedList<Integer> tem = new LinkedList<Integer>();
    public List<List<Integer>> combine(int n, int k) {
        find(n,k,1);
        return ans;
    }
    public void find(int n,int k,int index){
        if(k==tem.size()){
            LinkedList<Integer> path = new LinkedList<Integer>();
            path.addAll(tem);
            ans.add(path);
            return ;
        }
        for(int i = index;i<= n-(k-tem.size())+1;i++){
            tem.addLast(i);
            find(n,k,i+1);
            tem.removeLast();
        }
        return ;
    }
}

lc-216.组合总数3

easy，回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    List<List<Integer>> ans = new LinkedList<List<Integer>>();
    LinkedList<Integer> path = new LinkedList<Integer>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        find(1,n,k,0);
        return ans;

    }
    public void find(int cur,int n,int k,int sum){
        if(sum==n){
            if(path.size()==k){
                LinkedList<Integer> tem = new LinkedList<Integer>();
                tem.addAll(path);
                ans.add(tem);
                return ;
            }else{
                return ;
            }
        }else if(sum>n){
            return ;
        }
        for(int i = cur;i<=9&&(i+sum)<=n;i++){
            path.addLast(i);
            find(i+1,n,k,sum+i);
            path.removeLast();//剪枝处理
        }
        return ;
    }
}

lc-17.电话号码的字母组合

easy，穷举，递归，回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    String[] str = new String[]{
        "","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"
    };
    List<String> ans = new LinkedList<String>();
    StringBuffer ss = new StringBuffer();
    char[] c;
    public List<String> letterCombinations(String digits) {
        if(digits.length()==0) return ans;
        c = digits.toCharArray();
        find(0,ss);
        return ans;
    }
    public void find(int cur,StringBuffer s){
        if(cur==c.length){
            ans.add(ss.toString());
            return ;
        }
        char[] tem = str[c[cur]-'0'].toCharArray();
        for(char ch : tem){
            s.append(ch);
            find(cur+1,s);
            s.deleteCharAt(s.length()-1);
        }
        return ;
    }
}

lc-39.组合总和

easy，简单递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    List<List<Integer>> ans = new LinkedList<List<Integer>>();
    LinkedList<Integer> path = new LinkedList<Integer>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        find(candidates,0,0,target);
        return ans;

    }
    public void find(int nums[],int cur,int sum,int target){
        if(sum==target){
            LinkedList<Integer> tem = new LinkedList<Integer>();
            tem.addAll(path);
            ans.add(tem);
            return ;
        }else if(sum>target){
            return ;
        }
        for(int i = cur;i<nums.length;i++){
            path.addLast(nums[i]);
            find(nums,i,sum+nums[i],target);
            path.removeLast();
        }
        return ;
    }
}

lc-40.组合总和2

在1的基础上加上排序，同一层去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
     List<List<Integer>> ans = new LinkedList<List<Integer>>();
    LinkedList<Integer> path = new LinkedList<Integer>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);//增加排序
        find(candidates,0,0,target);
        return ans;
    }
        public void find(int nums[],int cur,int sum,int target){
        if(sum==target){
            LinkedList<Integer> tem = new LinkedList<Integer>();
            tem.addAll(path);
            ans.add(tem);
            return ;
        }else if(sum>target){
            return ;
        }
        for(int i = cur;i<nums.length;i++){
            if(i>cur&&nums[i]==nums[i-1]) continue; //同一层去重
            path.addLast(nums[i]);
            find(nums,i+1,sum+nums[i],target);//i+1，每个元素只使用一次
            path.removeLast();
        }
        return ;
    }
}

2022-1-27

lc-42.接雨水

单调栈方法，如果当前高度大于栈顶高度，则说明遇到了槽，将槽弹出，为底的高度，此时如果栈不为空，则再取栈顶，其值与当前值中较小的一个为横向槽的高度，计算横向槽的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int trap(int[] height) {
        Stack<Integer> stack = new Stack();
        int sum = 0;
        stack.push(0);
        for(int  i = 1;i<height.length;i++){
            while(!stack.isEmpty()&&height[i]>height[stack.peek()]){
                int mid = stack.pop();
                if(!stack.isEmpty()){
                    int h = Math.min(height[stack.peek()],height[i]) - height[mid];//gao
                    int w = i - stack.peek()-1;//di
                    sum = sum + h * w;
                }
            }
            stack.push(i);
        }
        return sum;
    }
}

动态规划，这里按照列去计算，获取每一列的左边的最大高度与右边的最大高度，以当前列的高度为底，宽为1，高度为两边最大高度较小值减去底的高度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) {
            return 0;
        }

        int[] leftMax = new int[n];//左边最大高度获取
        leftMax[0] = height[0];
        for (int i = 1; i < n; ++i) {
            leftMax[i] = Math.max(leftMax[i - 1], height[i]);
        }

        int[] rightMax = new int[n];//右边最大高度获取
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            rightMax[i] = Math.max(rightMax[i + 1], height[i]);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += Math.min(leftMax[i], rightMax[i]) - height[i];
        }
        return ans;
    }
}

lc-347.前K个高频元素

优先队列，做了太多遍了，这里主要学习一下Map的相关操作，以及进一步熟悉比较器Comparator的使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        
        Map<Integer,Integer> map = new HashMap<Integer,Integer>();
        for(int i : nums){
            map.put(i,map.getOrDefault(i,0)+1);
        }
        PriorityQueue<Map.Entry<Integer,Integer>> queue = new PriorityQueue(new Comparator(){
            @Override
            public int compare(Object o1, Object o2) {//注意这里必须是Object
                Map.Entry<Integer,Integer> m1 = (Map.Entry<Integer,Integer>)o1;
                Map.Entry<Integer,Integer> m2 = (Map.Entry<Integer,Integer>)o2;
                return m2.getValue()-m1.getValue();
            }
        }
        );
       Set<Map.Entry<Integer,Integer>> set = map.entrySet();
       for(Map.Entry<Integer,Integer> e : set){
           queue.add(e);
       }
       int[] ans = new int[k];
       for(int i = 0;i<k;i++){
           ans[i] = queue.poll().getKey();
       }
       return ans;

    }
}

lc-239.滑动窗口最大值

hard，使用双端队列实现，LinkedList可以提供栈，队列的很多功能！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        LinkedList<Integer> list = new LinkedList();//双向队列，可以同时在队首和对尾插入和删除
        int[] ans = new int[nums.length - k +1];
        for(int i = 0;i<k;i++){
            while(!list.isEmpty()&&nums[list.getLast()]<nums[i]){
                list.pollLast();
            }
            list.addLast(i);
        }
        ans[0] = nums[list.getFirst()];
        for(int i = k;i<nums.length;i++){
            while(!list.isEmpty()&&nums[list.getLast()]<nums[i]){
                list.pollLast();
            }//每次push的时候，都向队尾加，如果队尾的值小于需要添加的值，就移除，毕竟每次取的都是最大值，小的值直接除掉，这样队首的值肯定是最大的
            list.addLast(i);
            while(list.getFirst()<i-k+1){
                list.pollFirst();//最大值从队首取，并且需要保证在窗口范围内，不在就移除
            }
            ans[i-k+1] = nums[list.getFirst()];
        }
        return ans;
    }
}

2022-1-24

lc-150.逆波兰表达式求值

easy，用栈即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList<Integer>();
        int n = tokens.length;
        for (int i = 0; i < n; i++) {
            String token = tokens[i];
            if (isNumber(token)) {
                stack.push(Integer.parseInt(token));//String转为Integer
            } else {
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch (token) {
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                    default:
                }
            }
        }
        return stack.pop();
    }

    public boolean isNumber(String token) {
        return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
    }
}

lc-20.有效的括号

easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean isValid(String s) {
        if(s==null) return false;
        char[] c = s.toCharArray();
        Stack<Character> st = new Stack();
        int len = c.length;
        for(int i = 0;i<len;i++){
            if(c[i]=='{') {
                st.push('}');
            }else if(c[i]=='['){
                st.push(']');
            }else if(c[i]=='('){
                st.push(')');
            }else if(st.isEmpty()||st.peek()!=c[i]){
                return false;
            }else{
                st.pop();
            }
        }
        return st.isEmpty();

    }
}

lc-232.用栈实现队列

easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class MyQueue {
    Stack sin;
    Stack sout;
    public MyQueue() {
        this.sin = new Stack<Integer>();
        this.sout = new Stack<Integer>();
    }
    
    public void push(int x) {
        sin.push(x);
    }
    
    public int pop() {
        if(sout.isEmpty()){
            while(!sin.isEmpty()){
                sout.push(sin.pop());
            }
        }
        Integer a = (Integer)sout.pop();
        return a;
    }
    
    public int peek() {
         if(sout.isEmpty()){
            while(!sin.isEmpty()){
                sout.push(sin.pop());
            }
        }
        Integer a = (Integer)sout.peek();
        return a;
    }
    
    public boolean empty() {
        return sin.isEmpty()&&sout.isEmpty();
    }
}

lc-459.重复的字符串

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成，给定的字符只含有小写英文字符，并且长度不超过10000。

解题思路：求该字符串的前缀表，如果len % (len - next[len-1]) == 0，则说明可以由重复的子字符串构成。数组长度减去最长相等前后缀的长度相当于第一个重复子字符串的长度，也就是一个重复周期的长度，如果这个周期可以被整除，则说明整个数组就是这个周期的循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    int[] next;
    public void getNext(String s){
        char[] c = s.toCharArray();
        int len = c.length;
        next = new int[len];
        next[0] = 0;
        int j = 0;
        for(int i = 1; i<len;i++){
            while(j>0&&c[i] != c[j]){
                j = next[j-1];
            }
            if(c[i]==c[j]){
                j++;
            }
            next[i] = j;
        }
    }
    public boolean repeatedSubstringPattern(String s) {
        if(s==null||s.length()==0) return false;
        getNext(s);
        int len = s.length();
        if(next[len-1]!=0&&len%(len-next[len-1])==0) return true;
        else return false;
    }
}

2022-1-20

lc-344.反转字符串

easy，双指针。

lc-541.反转字符串2

easy，双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public String reverseStr(String s, int k) {
        int n = s.length();
        char[] arr = s.toCharArray();
        for (int i = 0; i < n; i += 2 * k) {
            reverse(arr, i, Math.min(i + k, n) - 1);
        }
        return new String(arr);
    }

    public void reverse(char[] arr, int left, int right) {
        while (left < right) {
            char temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;
            left++;
            right--;
        }
    }
}

lc-151.翻转字符串里的单词

mid，不难就是麻烦😓😖

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Solution {
    public String reverseWords(String s) {
        StringBuilder sb = trimSpaces(s);

        // 翻转字符串
        reverse(sb, 0, sb.length() - 1);

        // 翻转每个单词
        reverseEachWord(sb);

        return sb.toString();
    }

    public StringBuilder trimSpaces(String s) {
        int left = 0, right = s.length() - 1;
        // 去掉字符串开头的空白字符
        while (left <= right && s.charAt(left) == ' ') {
            ++left;
        }

        // 去掉字符串末尾的空白字符
        while (left <= right && s.charAt(right) == ' ') {
            --right;
        }

        // 将字符串间多余的空白字符去除
        StringBuilder sb = new StringBuilder();
        while (left <= right) {
            char c = s.charAt(left);

            if (c != ' ') {
                sb.append(c);
            } else if (sb.charAt(sb.length() - 1) != ' ') {
                sb.append(c);
            }

            ++left;
        }
        return sb;
    }

    public void reverse(StringBuilder sb, int left, int right) {
        while (left < right) {
            char tmp = sb.charAt(left);
            sb.setCharAt(left++, sb.charAt(right));
            sb.setCharAt(right--, tmp);
        }
    }

    public void reverseEachWord(StringBuilder sb) {
        int n = sb.length();
        int start = 0, end = 0;

        while (start < n) {
            // 循环至单词的末尾
            while (end < n && sb.charAt(end) != ' ') {
                ++end;
            }
            // 翻转单词
            reverse(sb, start, end - 1);
            // 更新start，去找下一个单词
            start = end + 1;
            ++end;
        }
    }
}

2022-1-19

lc-15.三数相加

mid，双指针法，先排序，从i开始，使用left和right两个指针去寻找i之后可能的情况，需要去重，需要考虑的很多情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        ArrayList<List<Integer>> ans = new ArrayList<List<Integer>> ();
        Arrays.sort(nums);
        for(int i = 0;i<nums.length - 2;i++){
            if(nums[i] > 0){
                break ; 
            }
            if(i > 0 && nums[i] == nums[i-1]){
                continue;//去重，往前判断去重，不要往后判断
            }
            int left = i+1;
            int right = nums.length - 1;
            while(right>left){
                int tem = nums[i] + nums[left] + nums[right];
                if(tem == 0){
                    ArrayList<Integer> temp = new ArrayList();
                    temp.add(nums[i]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    ans.add(temp);
                    while(right>left&&nums[right]==nums[right-1]){
                        right--;//去重 [-2,0,0,2,2]
                    }
                    while(right>left&&nums[left]==nums[left+1]){
                        left++;//去重 [-2,0,0,2,2]
                    }
                    right--;
                    left++;
                }else if(tem<0){
                    left++;
                }else if(tem>0){
                    right--;
                }
            }
        }
        return ans;

    }
}

lc-18.四数之和

mid，在三数之和的基础上，加一层循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        ArrayList<List<Integer>> ans = new ArrayList<List<Integer>> ();
        Arrays.sort(nums);
        for(int a = 0;a<nums.length;a++){
            if(a>0&&nums[a]==nums[a-1]){
                continue;
            }
            for(int b = a+1;b<nums.length;b++){
                if(b>a+1&&nums[b]==nums[b-1]){
                    continue;
                }
                int left = b+1;
                int right = nums.length-1;
                while(right>left){
                    int tem = nums[a] + nums[b] + nums[left] +nums[right];
                    if(tem==target){
                        ArrayList<Integer> temp = new ArrayList<Integer>();
                        temp.add(nums[a]);
                        temp.add(nums[b]);
                        temp.add(nums[left]);
                        temp.add(nums[right]);
                        ans.add(temp);
                        while(right>left&&nums[right]==nums[right-1]){
                            right--;
                        }
                        while(right>left&&nums[left]==nums[left+1]){
                            left++;
                        }
                        right--;
                        left++;
                    }else if(tem > target){
                        right--;
                    }else if(tem <target){
                        left++;
                    }
                }

            }
        }
        return ans;
    }
}

lc-454.四数相加2

mid，四个数组分成两组，然后使用哈希处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        HashMap<Integer,Integer> map = new HashMap();
        for(int a : nums1){
            for(int b : nums2){
                map.put(a+b, map.getOrDefault(a+b, 0) + 1);
            }
        }
        int count = 0;
        for(int c : nums3){
            for(int d : nums4){
                if(map.containsKey(0-c-d)){
                    count += map.get(0-c-d);
                }
            }
        }
        return count;
    }
}

lc-349.两个数组的交集

easy,重新熟悉一下迭代器iterator的用法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set = new HashSet();
        Set<Integer> ans = new HashSet();
        for(int i = 0;i<nums1.length;i++){
            set.add(nums1[i]);
        }
        for(int i =0;i<nums2.length;i++){
            if(set.contains(nums2[i])){
                ans.add(nums2[i]);
            }
        }
        Iterator<Integer> in = ans.iterator();
        int[] res = new int[ans.size()];
        int x = 0;
        while(in.hasNext()){
            res[x++] = in.next(); 
        }
        
        return res;
    }
}

lc-242.有效的字母异位词

easy，排序，然后一一比较，或者使用哈希表，记录每个字母出现的次数，遍历s，次数++，遍历t，次数–，最后看所有字母的次数是否为0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public boolean isAnagram(String s, String t) {
        if(s.length()!=t.length()) return false;
        char[] ss = s.toCharArray();
        char[] tt = t.toCharArray();
        Arrays.sort(ss);
        Arrays.sort(tt);
        for(int i = 0;i<ss.length;i++){
            if(ss[i]!=tt[i]){
                return false;
            }
        }
        return true;

    }
}

lc-669.修建二叉搜索树

easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root==null) return null;
        if(root.val<low){
            return trimBST(root.right,low,high);
        }
        if(root.val>high){
            return trimBST(root.left,low,high);
        }
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}

lc-108.构建平衡二叉搜索树

easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    int[] numss;
    public TreeNode sortedArrayToBST(int[] nums) {
        int len = nums.length;
        numss = nums;
        return build(0,len-1);
    }
    public TreeNode build(int left,int right){
        if(left>right) return null;
        int mid = left + (right-left)/2 ;
        TreeNode cur = new TreeNode(numss[mid]);
        cur.left = build(left,mid-1);
        cur.right = build(mid+1,right);
        return cur;
    }
}

2022-1-16

lc-14.最长公共前缀

easy，暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public String longestCommonPrefix(String[] strs) {
        int count = strs.length;
        if(count==1) return strs[0];
        int len = 0;
        while(true){
            int flag = 1;
            for(int i = 1;i<count;i++){
                if(len<strs[i-1].length()&&len<strs[i].length()){
                    if(strs[i].charAt(len)==strs[i-1].charAt(len)){
                        continue;
                    }else{
                        flag = 0;
                        break;
                    }
                }else{
                    flag = 0;
                    break;
                }
            }
            if(flag==0){
                break ;
            }
            len++;
        }
        if(len==0) return "";
        return strs[0].substring(0,len);

    }
}

lc-382.链表的随机节点

离谱题，人家用了一种蓄水池算法，只能说我见识浅陋了😅

image-20220116223302317

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    ListNode myhead;
    public Solution(ListNode head) {
        myhead = head;
    }    
    public int getRandom() {
        ListNode tem = myhead;
        Random random = new Random();
        int ans = tem.val;
        int len = 0;
        while(tem!=null){
            len++;
            if(random.nextInt(len)==0){
                ans = tem.val;
            }
            tem = tem.next;
        }
        return ans;
    }
}

lc-450.删除二叉搜索数中的节点

mid，最复杂的情况是被删除的节点的左右子树都存在，此时只需要将左子树接到右子树的最左边的节点的左边，返回右子树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return root;
        if(root.val==key){
            if(root.left==null) return root.right;
            else if(root.right==null) return root.left;
            else{ //删除的节点的左右子树均不为空
            //把左子树接到右子树的最左边的节点上，返回右子树即可
                TreeNode cur = root.right;
                while(cur.left!=null){
                    cur = cur.left;
                }
                cur.left = root.left;
                return root.right;
            }
        }
        if(key>root.val) {
            root.right = deleteNode(root.right,key);
        }else{
            root.left = deleteNode(root.left,key);
        }
        return root;
    }
}

lc-701.二叉搜索树中的插入操作

mid，只考虑最简单的插入方式，只插入到左子树为空或右子树为空且值满足条件的地方，不在中间插入，太麻烦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root==null) {
            root = new TreeNode(val);
            return root;
        }
        if(root.val > val){
            if(root.left!=null){
                root.left = insertIntoBST(root.left,val);
            }else{
                TreeNode tem = new TreeNode(val);
                tem.left = null;
                tem.right=null;
                root.left = tem;
                return root;
            }
        }else{
             if(root.right!=null){
                root.right = insertIntoBST(root.right,val);
            }else{
                TreeNode tem = new TreeNode(val);
                tem.left = null;
                tem.right=null;
                root.right = tem;
                return root;
            }       
        }
        return root;
    }
}

lc-236.二叉树的最近公共祖先

后序遍历，自底向上回溯。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==p||root==q||root==null) return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left==null&&right!=null) return right;
        else if(left!=null&&right==null) return left;
        else if(left!=null&&right!=null) return root;
        else return null;
    }
}

lc-235.二叉搜索树的最近公共祖先

easy

1
2
3
4
5
6
7
8
9
10
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==p||root==q ||root==null) return root;
        if(root.val>p.val&&root.val>q.val) return lowestCommonAncestor(root.left,p,q);
        else if(root.val<p.val&&root.val<q.val) return lowestCommonAncestor(root.right,p,q);
        else if(root.val>p.val&&root.val<q.val) return root;
        else if(root.val<p.val&&root.val>q.val) return root;
        else return null;
    }
}

2022-1-15

字节后端训练营笔试。

编程题三道。

  • 细胞分裂，相对简单
  • 判断一个数是否是另一个数的最小相似数，把整数当做字符串处理，排序之后对应比较即可
  • 通关所需的最少关卡数，a了0.8，滑动窗口法，情况没考虑全面😭😭😭

2022-1-14

lc-7.整数反转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            rev = rev * 10 + digit;
        }
        return rev;
    }
}

lc-6.Z字型变换

mid.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public String convert(String s, int numRows) {
        if(numRows==1) return s;
        StringBuilder[] ss = new StringBuilder[Math.min(s.length(),numRows)];
        for(int i = 0;i<ss.length;i++){
            ss[i] = new StringBuilder();
        }
        int row = 0;
       int flag = -1;
        for(char c : s.toCharArray()){
            ss[row].append(c);
            if(row==0||row==(ss.length-1)) flag = -flag;
            row +=flag;
        }
        StringBuilder ans = new StringBuilder();
        for(StringBuilder ls : ss){
            ans.append(ls);
        }
        return ans.toString();
    }
}

lc-9.回文数

easy。

lc-373.查找和最小的K对数字

跟之前的丑数一样，类似多路归并问题，使用优先队列（小根堆）解决，套路都是一样的。

针对nums1中的每个元素，维护一个元素对应的nums2中的元素索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        if(k==0||nums1.length==0||nums2.length==0) return ans;
        PriorityQueue<int[]> queue = new PriorityQueue<>(k, (o1, o2)->{
            return nums1[o1[0]] + nums2[o1[1]] - nums1[o2[0]] - nums2[o2[1]];
        });//学习一下这里的比较器写法。
        for(int i = 0;i<nums1.length;i++){
            queue.add(new int[]{i,0});
        }
        int len2 = nums2.length;
        while(k!=0&&!queue.isEmpty()){
            int[] tem = queue.poll();
            List<Integer> temp = new ArrayList();
            temp.add(nums1[tem[0]]);
            temp.add(nums2[tem[1]]);
            ans.add(temp);
            if(tem[1]+1<len2){
                queue.add(new int[]{tem[0],tem[1]+1});
            }
            k--;
        }
        return ans;
    }
}

2022-1-12

剑指29.顺时针打印矩阵

跟之前打印螺旋矩阵差不多，主要是怎么遍历，判断临界条件，要把各种情况考虑全面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if(matrix.length==0) return new int[0];
        int hang = matrix.length;
        int lie = matrix[0].length;
        int used = 0;
        int[]  ans = new int[hang*lie];
        int x = 0,i = 0,j = 0;
        while(used*2<Math.min(hang,lie)){
            i = used;
            j = used;
            for(j = used;j<lie-used-1;j++){
                ans[x++] = matrix[i][j];
            }
            for(i = used;i<hang-used-1;i++){
                ans[x++] = matrix[i][j]; 
            }
            if(i==used||j==used){/////重点！！！！处理特殊情况，防止数组下标溢出
                ans[x++] = matrix[i][j];
                break ;
            }
            for( ;j > used;j--){
                ans[x++] = matrix[i][j];
            }
            for( ; i >used;i--){
                ans[x++] = matrix[i][j];
            }
            used++;
        }
        if(x!=hang*lie){
            ans[x] = matrix[hang/2][lie/2];
        }
        return ans;
    }
}

lc-96.不同的二叉搜索树

mid，简单动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numTrees(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        int[] dp = new int[n+2];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i<=n;i++){
            dp[i] = 0;
            for(int j = 1;j<=i;j++){
                dp[i] =dp[i]+dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}

lc-95.不同的二叉搜索树2

mid，递归处理。

lc95

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public List<TreeNode> generateTrees(int n) {
            if(n == 0) return new LinkedList<TreeNode>();
            return  gen(1,n);
    }
    public List<TreeNode> gen(int start,int end){
         List<TreeNode> ans = new LinkedList<TreeNode>();
         if(start > end){
             ans.add(null);
             return ans;
         }
         for(int i = start;i<=end;i++){
             List<TreeNode> leftAns = gen(start,i-1);
             List<TreeNode> rightAns = gen(i+1,end);
             for(TreeNode left : leftAns){
                 for(TreeNode right : rightAns){
                     TreeNode cur = new TreeNode(i);
                     cur.left = left;
                     cur.right = right;
                     ans.add(cur);
                 }
             }

         }
         return ans;
    }
}

2022-1-11

lc-501.二叉搜索树中的众数

easy,中间保存和替换结果错了好多次。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    int max = 0;
    int count = 0;
    TreeNode pre = null;
    ArrayList<Integer> ans;
    public int[] findMode(TreeNode root) {
        ans = new ArrayList();
        find(root);
        int len = ans.size();
        int[] anss= new int[len];
        int i = 0;
        for(Integer a : ans){
            anss[i++] = a;
        }
        return anss;
    }
    public void find(TreeNode root){

        if(root==null) return ;
        find(root.left);

        if(pre!=null&&pre.val==root.val){
            count++;

        }else{
            count=1;
        }
        if(count>max){
            max = count;
            ans.clear();
            ans.add(root.val);
        }
        else if(count==max){
            ans.add(root.val);
        }
        pre = root;
        find(root.right);
        return ;
    }
}

lc-98.验证二叉搜索树

mid，注意这个pre的作用，很妙。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    TreeNode pre = null; //pre始终代表上一个访问的节点，而访问节点的顺序是按照从小到大访问的，即中序遍历的方式
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        boolean left = isValidBST(root.left);//访问左子树
        
        if(pre!=null&&pre.val>=root.val) return false; //访问当前树
        pre = root;//访问完当前之后，pre就变成了当前的root
        boolean right = isValidBST(root.right);//访问右子树

        return left&&right;
    }
 
}

lc-530.二叉搜索树的最小绝对差

easy，借鉴上一题，使用pre记录上一个节点，中序遍历访问节点，每次取当前节点和pre 的差值，保留更小的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    int  result = 1000000;
    TreeNode pre;
    public int getMinimumDifference(TreeNode root) {
        if(root==null) return 0;
        getMinimumDifference(root.left);
        if(pre!=null){
            result = Math.min(result,root.val-pre.val);
        }
        pre = root;
        getMinimumDifference(root.right);
        return result;
    }
}

lc-700.二叉树中的搜索

easy，递归。

1
2
3
4
5
6
7
8
9
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null) return null;
        if(root.val==val) return root;
        if(root.val>val) return searchBST(root.left,val);
        if(root.val<val) return searchBST(root.right,val);
        return null;
    }
}

lc-617.合并二叉树

easy,简单递归即可。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1==null) return root2;
        if(root2==null) return root1;

        root1.val += root2.val;
        root1.left = mergeTrees(root1.left,root2.left);
        root1.right = mergeTrees(root1.right,root2.right);
        return root1;
    }
}

lc-105.根据前序和中序遍历构造二叉树

mid,根据前序遍历确定根节点的值，根据根节点的值和中序遍历的到左右子树的范围，然后递归处理。

主要难点在于递归时数组下标的确定！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    int[] pre;
    HashMap<Integer,Integer> map;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(inorder.length<=0||preorder.length<=0) return null;
        pre = preorder;
        map = new HashMap();
        for(int i = 0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        TreeNode root = new TreeNode(preorder[0]);
        int rootindex = map.get(root.val);
        build(root,0,0,rootindex-1,rootindex+1,inorder.length-1);
        return root;
    }
    public void build(TreeNode root,int rootpredex,int lefts,int lefte,int rights,int righte){ //根节点，前序根的位置，中序左子树范围，中序右子树范围
        //左子树
        if(lefts>lefte){
            root.left=null;
        }else{
            root.left = new TreeNode(pre[rootpredex+1]);//前序求左孩子值
            int leftindex = map.get(root.left.val);//中序左孩子位置
            build(root.left,rootpredex+1,lefts,leftindex-1,leftindex+1,lefte);//左孩子，左孩子前序位置，新左子树中序，新右子树中序
        }
        //右子树
        if(rights>righte){
            root.right=null;
        }else{
            int rightpredex = 0;
            if(lefts>lefte){  //通过左子树的长度去找右子树的根节点
                 rightpredex = rootpredex+1;
            }else{
                 rightpredex = rootpredex+lefte-lefts+2;
            }
            root.right = new TreeNode(pre[rightpredex]);//前序求右孩子值
            int rightindex = map.get(root.right.val);//中序右孩子位置
            build(root.right,rightpredex,rights,rightindex-1,rightindex+1,righte);
        }
        return ;
    }
}

2022-1-9

lc-112.路径总和1

easy，递归加回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root ==null) return false;
        return find(root,targetSum-root.val);
    }
    public boolean find(TreeNode root,int sum){
        if(root.left==null&&root.right==null&&sum==0) return true;
        if(root.left==null&&root.right==null) return false;
        if(root.left!=null){
            if(find(root.left,sum-root.left.val)) return true;
        }
        if(root.right!=null){
            if(find(root.right,sum-root.right.val)) return true;
        }
        return false;
              
    }
}

lc-113.路径总和2

注意向List中添加的节点到底是父节点还是子节点！！！！

List<List < Integer >>中里面的List只是一个引用，因此每次找到一条路径，都要把当前的路径复制一份到另一个新的List中，把新的List加到ans中，不然之后的遍历会把保存中途路径的path更改掉！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    ArrayList<List<Integer>> ans;
    List<Integer> path;
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        ans = new  ArrayList<List<Integer>>();
        if(root==null) return ans;
        path = new ArrayList<Integer>();
        path.add(root.val);
        find(root,targetSum-root.val);
        return ans;
    }
    public void find(TreeNode root,int sum){
        if(root.left==null&&root.right==null&&sum==0){
            List<Integer> tem = new ArrayList<Integer>(); //新申请一个List然后添加进去
            tem.addAll(path);
            ans.add(tem);
            return ;           
        }
        if(root.left==null&&root.right==null){
            return ;
        }
        if(root.left!=null){
            path.add(root.left.val);
            find(root.left,sum-root.left.val);
            int len = path.size();
            path.remove(len-1);
        }
        if(root.right!=null){
            path.add(root.right.val);
            find(root.right,sum-root.right.val);
            int len = path.size();
            path.remove(len-1);
        }
        return ;
    }
}

2022-1-8

lc-102.二叉树最大深度

1
2
3
4
5
6
class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));
    }
}

lc-111.二叉树最小深度

​ easy。

​ 递归法：

1
2
3
4
5
6
7
8
class Solution {
    public int minDepth(TreeNode root) {
        if(root==null) return 0;
        if(root.left==null&&root.right!=null) return 1+minDepth(root.right);
        if(root.right==null&&root.left!=null) return 1+minDepth(root.left);
        return 1 + Math.min(minDepth(root.right),minDepth(root.left)); 
    }
}

​ 迭代法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.add(root);
        int depth = 1;
        while(!q.isEmpty()){  //每遍历一层，深度加一，直到遇到第一个叶子结点
            int len = q.size();
            for(int i = 1;i<=len;i++){
                TreeNode t = q.remove();
                if(t.left==null&&t.right==null) return depth;
                if(t.left!=null) q.add(t.left);
                if(t.right!=null) q.add(t.right);
            }
            depth++;
        }
        return depth;
    }
}

lc-110.平衡二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        if(depth(root)==-1) return false;
        return true;
    }
    public int depth(TreeNode root){
        if(root==null) return 0;
        int left = depth(root.left);
        int right = depth(root.right);
        if(left==-1||right==-1) return -1;
        if(Math.abs(left-right)>1) return -1;
        return 1+Math.max(left,right);
    }
}

lc-257.二叉树的所有路径

​ easy，深度优先+回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    ArrayList<String> ans;
    public List<String> binaryTreePaths(TreeNode root) {
        if(root==null) return ans;
        ans = new ArrayList<String>();
        StringBuffer s = new StringBuffer();
        s.append(""+root.val);
        if(root.left==null&&root.right==null) {
            ans.add(s.toString());
        }else{
            find(root.left,s);
            find(root.right,s);
        }   
        return ans;
    }
    public void find(TreeNode root,StringBuffer s){
        if(root==null) return ;
        int old = s.length();
        s.append("->");
        s.append(""+root.val);
        if(root.left==null&&root.right==null) {
            ans.add(s.toString());
        }else{
            find(root.left,s);
            find(root.right,s);
        }    
        int nnew = s.length();
        s.delete(old,nnew);//左开右闭
        return ;
    }
}

2022-1-7

HOT-11.盛水最多的容器

​ mid，不看题解想不出系列😅

​ 双指针法，起初分别指向最前面和最后面，然后移动指针。移动原理如下：

​ 一开始两个指针一个指向开头一个指向结尾，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，在这种情况下想要让容器盛水变多，就只有在容器的高上下功夫。 那我们该如何决策哪个指针移动呢？我们能够发现不管是左指针向右移动一位，还是右指针向左移动一位，容器的底都是一样的，都比原来减少了 1。这种情况下我们想要让指针移动后的容器面积增大，就要使移动后的容器的高尽量大，所以我们选择指针所指的高较小的那个指针进行移动，这样我们就保留了容器较高的那条边，放弃了较小的那条边，以获得有更高的边的机会。

​ 总之，每次都试图找更大的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxArea(int[] height) {
        if(height.length==0) return 0;
        int left = 0,right = height.length-1;
        int max = 0;
        while(left<right){
            if(height[left]<height[right]){
                max = Math.max(max,(right-left)*height[left]);
                left++;
            }else{
                max = Math.max(max,(right-left)*height[right]);
                right--;
            }
        }
        return max;
    }
}

HOT-3.无重复字符的最长字串

​ mid，滑动窗口。

​ 每次尝试向窗口右侧添加新值，如果想要添加的已经在窗口中存在，则不添加，并把窗口最左的的字符拿出去即可，每次循环更新最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s==null) return 0;
        char[] c = s.toCharArray();
        if(c.length==0) return 0;
        int max = 1;
        Set<Character> q = new HashSet<Character>();
        q.add(c[0]);
        for(int i = 0,j=1;i<c.length-1&&j<c.length;){
            while((j<=c.length-1)&&!q.contains(c[j])){
                q.add(c[j]);
                j++;
            }
            if((j-i)>max) {max = j-i;}
            q.remove(c[i]);
            i++;
        }
        return max;
    }
}

2022-1-4

每天不间断开始！！！

复习二叉树前中后序的遍历，迭代式就按照统一迭代做了，就只记住这一种，方法实在太多了，记住一种即可。

前序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import java.util.ArrayList;
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> s = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        TreeNode tem = root;

        while(tem != null || !(s.isEmpty())){
            while(tem !=null){
                s.push(tem);
                ans.add(tem.val);
                tem = tem.left;
            }
            if(!s.isEmpty()){
                tem = s.pop();
                tem = tem.right;
            }
        }
        return ans;

    }
}

统一迭代式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.ArrayList;
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        
        Stack<TreeNode> s = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        TreeNode tem = root;
        if(root==null) return ans;
        s.push(root);
        while(!s.isEmpty()){ //先push右，然后push左，然后push中，紧跟一个null，读到null就说明读到中了，这样先读一个null，此时栈顶是中，读取值，然后左，处理左，最后读右，处理右
            tem = s.pop();//对每一个中，先把他pop出来，在去处理左中右
            if(tem != null){
                if(tem.right!=null) s.push(tem.right);//右
                if(tem.left!=null) s.push(tem.left);//左
                s.push(tem);//中
                s.push(null);
            }else{
                tem = s.pop();
                ans.add(tem.val);
            }
        }
        return ans;
    }
}

中序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import java.util.ArrayList;
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> s = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        TreeNode tem = root;

        while(tem != null || !(s.isEmpty())){
            while(tem !=null){
                s.push(tem);
                tem = tem.left;
            }
            if(!s.isEmpty()){
                tem = s.pop();
                ans.add(tem.val);
                tem = tem.right;
            }
        }
        return ans;

    }
}

统一式迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.ArrayList;
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        
        Stack<TreeNode> s = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        TreeNode tem = root;
        if(root==null) return ans;
        s.push(root);
        while(!s.isEmpty()){ //先push右，然后push中，紧跟一个null，读到null就说明读到中了，然后push左，这样先读左，左子树读完，先读一个null，此时栈顶是中，读取值
            tem = s.pop();//对每一个中，先把他pop出来，在去处理左中右
            if(tem != null){
                if(tem.right!=null) s.push(tem.right);//右
                s.push(tem);//中
                s.push(null);
                if(tem.left!=null) s.push(tem.left);//左
            }else{
                tem = s.pop();
                ans.add(tem.val);
            }
        }
        return ans;
    }
}

后序遍历：

统一迭代式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.ArrayList;
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        
        Stack<TreeNode> s = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        TreeNode tem = root;
        if(root==null) return ans;
        s.push(root);
        while(!s.isEmpty()){ //先push中，紧跟一个null，读到null就说明读到中了，然后push右，然后push左，这样先读左，左子树读完，然后读右，右子树处理完，然后读一个null，此时栈顶是中，读取值
            tem = s.pop();//对每一个中，先把他pop出来，在去处理左中右
            if(tem != null){
                s.push(tem); //中
                s.push(null);
                if(tem.right!=null) s.push(tem.right);//右
                if(tem.left!=null) s.push(tem.left);//左
            }else{
                tem = s.pop();
                ans.add(tem.val);
            }
        }
        return ans;
    }
}

层序遍历：写太多了，吐了，不写。

2021-12-21

链表专题。

  • lc203.移除链表元素

    easy，但需要注意next值的传递。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode ahead = new ListNode(0);
        ahead.next = head;
        ListNode tem = ahead;
       while(tem.next!=null){
           if(tem.next.val==val){
               tem.next = tem.next.next;  //这里改了下一个节点之后，不能直接把tem 等于新的下一个节点，新的下一个节点可能为空或需要删除的值。
           }else{
               tem = tem.next;
           }
       }
        return ahead.next;

    }
}

  • lc707.设计链表

    mid，涵盖了基本的链表操作，还是要注意判断怎么搜索到第index个，容易出错；

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    class MyLinkedList {
        node ahead;
        int size;
        node tail;

        public MyLinkedList() {
            ahead = new node();
            size = 0;
            tail = null;
        }
        
        public int get(int index) {
            if(index > (size -1)||index < 0){
                return -1;
            }
            else{
                node tem = ahead.next;
                while((index--)!=0){
                    tem = tem.next;
                }
                return tem.val;
            }
        }
        
        public void addAtHead(int val) {
            node tem = new node(val);
            tem.next = ahead.next;
            ahead.next = tem;
            if(tail==null){
                tail = tem;
            }
            size++;
        }
        
        public void addAtTail(int val) {
            node tem = new node(val);
            if(tail==null){
                ahead.next = tem;
                tem.next = null;
                tail = tem;
            }else{
                tail.next = tem;
                tem.next = null;
                tail = tem;
            }
            size++;
        }
        
        public void addAtIndex(int index, int val) {
            if(index>size){
                return ;
            }
            if(index<=0){
                addAtHead(val);
                return ;
            }
            if(index==size){
                addAtTail(val);
                return ;
            }
            node tem = ahead;
            while((index--)!=0){
                tem = tem.next;
            }
            node t = new node(val);
            t.next = tem.next;
            tem.next = t;
            size++;
        }
        
        public void deleteAtIndex(int index) {
            if(index>(size-1) || index <0){
                return ;
            }
            node tem = ahead;
            while((index--)!=0){
                tem = tem.next;
            }
            if(tem.next==tail){
                tem.next = null;
                tail = tem;
                size--;
            }else{
                tem.next  = tem.next.next;
                size--;
            }
        }
    }

    class node{
        int val;
        node next;
        node(){

        }
        node(int val){
            this.val = val;
        }
    }

  • lc206 反转链表

    easy，双指针法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null) return null;
        ListNode pre,cur,tem;
        pre = head;
        cur = head.next;
        pre.next = null;
        while(cur!=null){
            tem = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tem;
        }
        return pre;
    }
}

  • lc92.反转链表2

    mid，虽然是单向，找一个数组存一下就行，没想到更好的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if(head==null) return null;
        ListNode data[] = new ListNode[right-left+1];
        ListNode tem = head;
        int x = right - left;
        while(left > 1){
            tem = tem.next;
            left--;
        }
        while(x>=0){
            data[x] = tem;
            tem = tem.next;
            x--;
        }
        int i = 0,j=data.length - 1;
        while(i<j){
            x = data[i].val;
            data[i].val = data[j].val;
            data[j].val = x;
            i++;
            j--;
        }
        return head;
    }
}

​ 双指针解法，太tm强了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//g指向left前的那一个节点，p执行left，然后逐个把p后面的节点删除，并插入到g后面，直到right插到g后面
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if(head==null) return null;
        ListNode ahead = new ListNode();
        ahead.next = head;
        ListNode g = ahead,p,tem;
        int x = right - left;
        while(left > 1){
            g = g.next;
            left--;
        }
        p = g.next;
        while(x>0){
            if(p.next==null){
                break;
            }
            tem = p.next;
            p.next = tem.next;
            tem.next = g.next;
            g.next = tem;
            x--;
        }
        return ahead.next;        
    }
}

  • lc142.环形链表2

    mid，如果存在环，快慢指针会在环中相遇，分别从相遇点和链表头开始以相同的速度遍历，将会在入口点相遇，证明看书或题解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head==null) return null;
        if(head.next==null) return null;
        ListNode fast = head,slow=head;
        while(fast!=null&&fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow==fast){
                ListNode tem1 = head,tem2 = slow;
                while(tem1!=tem2){
                    tem1 = tem1.next;
                    tem2 = tem2.next;
                }
                return tem1;
            }
        }
        return null;        
    }
}

  • lc23.合并K个升序链表

    hard，简单的hard，经典的K路归并问题，使用优先队列就可以解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode ahead = new ListNode();
        if(lists == null) return null;
        if(lists.length==0) return null;
        PriorityQueue<ListNode> queue = new PriorityQueue<ListNode>(new Comparator<ListNode>(){
            @Override
            public int compare(ListNode l1,ListNode l2){
                return l1.val - l2.val;
            }
        });
        for(int i = 0;i<lists.length;i++){
            if(lists[i]!=null){
                queue.add(lists[i]);
            }
        }
        ListNode index = ahead;
        while(!queue.isEmpty()){
            ListNode x = queue.poll();
            index.next = x;
            index = index.next;
            if(x.next!=null){
                queue.add(x.next);
            }
        }
        index.next = null;
        return ahead.next;
    }
}

今天写了六道呢！😲😲😲

2021-12-19

周赛。

  • #2108.找出数组中的第一个回文字符串

  • #2109.向字符串添加空格

    学会用StringBuffer！！！，不要老是在字符串，字符数组的转换上出问题！！

  • #2110.股票平滑下跌的阶段

    动态规划，找递推式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public long getDescentPeriods(int[] prices) {
        long count = 1;
        long[] dp = new long[prices.length];
        dp[0] = 1;
        for(int i = 1;i<prices.length;i++){
            if(prices[i] == prices[i-1]-1){
                count++;
                dp[i] = dp[i-1] +count;
            }else{
                count=1;
                dp[i] = dp[i-1] +count;
            }
        }
        return dp[prices.length-1];
    }
}

  • #2111.使数组K递增的最少操作次数

    求最少操作次数就是对每一类的数组求他的最长不降子序列，数组长度减去该子序列的长度就是最少的操作次数。

    下面的代码还有一些问题，求最长不降子序列的复杂度是O(n2)，有更好的O(nlogn)的解法，有时间再改上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int kIncreasing(int[] arr, int k) {
        int length = arr.length;
        int ans = 0;
        int loop = length/k;
        int r = length%k;
        int count = 0;
        if(length == 100000 && arr[0] ==100000) return 99999;
        for(int i = 0;i <k;i++){
          if(i<r) {
            count = loop + 1;
          }else{
              count = loop;
          }
            ans  = ans + count - find(arr,i,k,count);
        }
        return ans;
    }

    public int find(int[] nums,int i,int k,int loop){

        int[] dp = new int[loop];
        int max = -1;
        for(int j = 0;j<loop;j++){
            dp[j] = 1;
            for(int x = j-1;x>=0;x--){
                if(nums[i+j*k]>=nums[i+x*k]){
                    dp[j] = Math.max(dp[x]+1,dp[j]);
                }
                if(dp[j] > x){
                    break;
                }
            }
            max = Math.max(max,dp[j]);
        }
        return max;
    }
}

2021-12-18

nmd，复习不完也得刷题。跟着代码随想录的书把算法知识过一遍。

  • lc704.二分查找

    复习二分查找，注意边界处理。

  • lc27.移除元素

    学习双指针的方法，利用快慢指针实现后续元素的前移。

  • lc209.长度最小的子数组

    学习滑动窗口法，利用滑动窗口遍历所有情况，而且只遍历一遍，O(n)。

  • lc59.螺旋矩阵二

    练习对边界条件的处理，采用统一的边界处理方式，全部左闭右开，不然容易到处出BUG。

  • lc4.寻找两个有序数组的中位数

    hard，全靠题解，通过二分法来排除不符合的元素。硬背。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    class Solution {
        public double findMedianSortedArrays(int[] nums1, int[] nums2) {
            int m = nums1.length,n=nums2.length;
            if((m+n)%2==1){
                return (double) findk(nums1,nums2,(m+n)/2 + 1);
            }else{
                return (findk(nums1,nums2,(m+n)/2 + 1) +findk(nums1,nums2,(m+n)/2))/2.0;
            }
        }
        public int findk(int[] nums1,int[] nums2,int k){
            int index1 = 0,index2=0;
            int length1 = nums1.length,length2 = nums2.length;

            while (true){
                if(index1 == length1) return nums2[index2 + k - 1];
                if(index2 == length2) return nums1[index1 + k - 1];
                if(k==1) return Math.min(nums1[index1],nums2[index2]);

                int x = k/2;
                int n1 = Math.min(index1+x-1,length1-1);
                int n2 = Math.min(index2+x-1,length2-1);

                int p1 = nums1[n1],p2 = nums2[n2];
                if(p1 < p2){
                    k = k - (n1 - index1 +1 );
                    index1 = n1 + 1;  
                }else{
                    k = k - (n2 - index2 +1 );
                    index2 = n2 + 1;  
                }
            }
        }
    }

2021-11-30

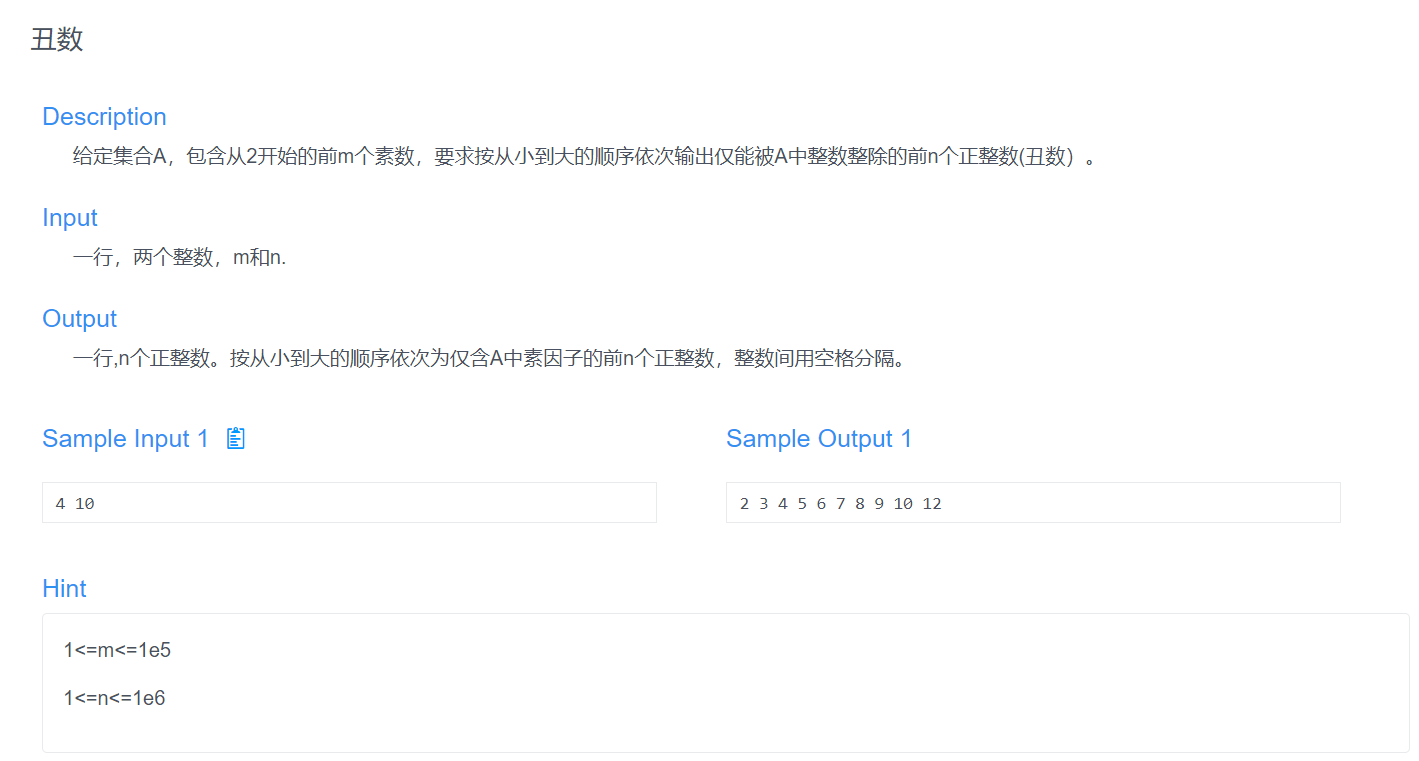
  • OJ.丑数

    丑数

    首先，根据输入，得到前n个素数，获得素数的方法有很多，时间复杂度各不相同，最快的应当是筛法求素数，但我不会😅😅，所以就采用笨一点的方法，从2和3开始依次往后枚举，如果这个数不能被前面的素数整除，那么他就是下一个素数，对于一个正整数n，判断能不能被从2到根号n范围内的素数整除即可。

    得到所有的素数之后，接下来就是求前n个丑数，基本的思路如下：

    假设前m个素数保存在数组primes中，对于一个丑数a,他一定是由小于他的丑数乘上素数集合primes中的一个元素得到，假设现在素数集合里只有2,3,5,用dp数组保存从小到大的丑数，dp[0]为1.

    对于最小的丑数，是从1 * 2, 1 * 3,1 * 5中取最小的一个，这里是2，则2就是dp[1]的值

    1
    dp[] = {1,2}

    那么接下来的丑数，应该是从2 * 2,1 * 3,1 * 5中取最小，是3，则dp[2] = 3

    1
    dp[] = {1,2,3}

    同理，下一个丑数是从2 * 2,2 * 3,1 * 5中取最小是4，则dp[3] = 4

    1
    dp[] = {1,2,3,4}

    继续下一个就是从3 * 2,2 * 3,1 * 5中取最小是5，则dp[4] = 5

    1
    dp[] = {1,2,3,4,5}

​ ···········································

于是，对于每一次取最小时，最小值的来源就来自于素数集合中的每一个素数，乘上他所对应的一个dp中的丑数，初始情况，每一个素数都乘dp[0]，dp[0]为1，在相乘之后的结果中，某一 个素数与dp中对应值相乘的结果最小，则将这个最小的结果加入dp数组，同时这个素数下一次相乘时对应的dp中的值应该是本次相乘的对应值的后一个。

因此，我们使用一个数组p来保存第i个素数对应的dp中元素的索引，初始情况，所有素数对应dp中的索引为0，即p数组中所有的值均为0，如果该素数与dp[0]相乘的结果是本次最小的，则将结果加入dp，同时将该素数对应的索引+1，比如一开始加入丑数2时，p[1]++（2是第一个素数），则p[1] = 1，所以下一次相乘取最小时，2要乘以dp[p[1]] ，即dp[1]。

因此求前n个丑数的步骤如下：

1
2
3
4
5
1.计算dp[p[i]]*primes[i],primes[i]表示第i个素数的值，p[i]表示第i个素数的相乘对象在dp中的索引，则dp[p[i]]，就是本次第i个素数的相乘对象。
2.求出最小的dp[p[i]]*primes[i]
  如果他的值比dp素组末尾的最大丑数大，那么他就是新的最大的丑数，加入到dp的最后，同时p[i]++,第i个素数下一次的相乘对象，是比本次相乘对象大的下一个丑数
  如果他的值与dp数组末尾的最大丑数相等，说明这个值已经存在了，就不用加入到dp数组中，但是也要把这个素数对应的索引值加一，即p[i]++
3.循环进行前两步，不断求出新的丑数，直到求出n个丑数

考虑到时间限制，在每一轮求出最小的dp[p[i]]*primes[i]时，使用最小堆求最小值，最小堆中的节点包含两个值，一个是index，表示这个节点对应的是哪一个素数，另一个是value，表示该节点的值的大小。

先将所有的primes[i]加入堆，接下来开始循环：

每次循环,取出堆中value最小的值，判断是否比上一个丑数大，如果大，则将本次的value加入dp，同时第index个素数的索引值加一，即p[index]++,然后把第index个素数新的dp[p[index]]*primes[index]的值加入到堆中，接着下一轮循环。

如果本次取出的堆中的最小值，与上一个丑数相同，则不必将其加入dp数组中，只把他对应的素数的索引加1，即p[index]++，然后把新的dp[p[index]]*primes[index]的值加入到堆中，接着下一轮循环。

在最小堆的数据，就是前m个素数与他所对应的dp中的某个丑数的乘积，每次取出一个dp[p[i]] * primes[i]，就要把新的dp[p[i]] * primes[i]加进去。

最终代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <iostream>
#include <math.h>
using namespace std;
unsigned long long p[100010];//每个素数索引
unsigned long long dp[1000010];//保存前n个
unsigned long long primes[100010];//前m个素数
struct Heap {
    unsigned long long index;
    unsigned long long value;
}heap[1000010],*a;
////////////最小堆的相关操作函数
int hs = 0;
void sink(int p) {
    int q = p << 1;
    unsigned long long a = heap[p].value, b = heap[p].index;
    while (q <= hs) {
        if (q < hs && heap[q + 1].value < heap[q].value) q++;
        if (heap[q].value >= a) break;
        heap[p].index = heap[q].index;
        heap[p].value = heap[q].value;
        p = q;
        q = p << 1;
    }
    heap[p].value = a;
    heap[p].index = b;
}
void swim(int p) {
    int q = p >> 1;
    unsigned long long a = heap[p].value, b = heap[p].index;
    while (q && a < heap[q].value) {
        heap[p].index = heap[q].index;
        heap[p].value = heap[q].value;
        p = q;
        q = p >> 1;
    }
    heap[p].value = a;
    heap[p].index = b;
}
void insert(Heap* a) {
    hs++;
    heap[hs].index= a->index;
    heap[hs].value = a->value;
    swim(hs);
}
Heap getmin() {
    Heap r = heap[1];
    heap[1] = heap[hs--];
    sink(1);
    return r;
}
///////////////////////////////////////

int main() {
    int m, n;
    scanf("%d%d", &m, &n);
    primes[1] = 2;
    primes[2] = 3;
    int tot = 2;
    for (int i = 5; tot < m; i++) {
        bool is = true;
        for (int j = 1; j <= tot && primes[j] <= sqrt(i); j++) {
            if (i % primes[j] == 0) {
                is = false;
                break;
            }
        }
        if (!is) continue;
        primes[++tot] = i;
    }////求出前m个素数
    dp[0] = 1;
    a = (Heap*)malloc(sizeof(Heap));
    for (int i = 1; i <= m; i++) {  
        a->index = i;
        a->value = primes[i];
        insert(a); //把dp[p[i]]*primes[i]的值加入堆，第一次p[i]均为0，dp[0]为1
    }
    tot = 0;
    Heap min;
    for (int i = 1; tot < n; i++) {
        min = getmin();
        if (min.value > dp[tot]) {
            dp[++tot] = min.value; //新的丑数加入dp 
            p[min.index]++; //对应索引后移
            min.value = dp[p[min.index]] * primes[min.index];
            insert(&min); //将新的乘积加入堆
            printf("%llu", dp[tot]);
            if (tot == n)  printf("\n");
            else    printf(" ");
        }
        else {//不必加入dp，但要把对应索引后移，将新的值加入堆
            p[min.index]++;
            min.value = dp[p[min.index]] * primes[min.index];
            insert(&min);
        }
    }

 }

2021-11-28

我也想刷题啊，可为什么还有那么多事啊😭😭😭😭

  • OJ.奶牛的食物

    奶牛的食物

    一道状态压缩DP的经典题型，起初的思路就是DP，但是不知道怎么DP😭😭

    个人理解，状态压缩DP就是将一个状态表现成一个数位0或1，对应某一块地的用还是不用，而一个数值包含多个位，就可以表示一组状态。

    因此，在这道题中，我们就可以使用一个int值来表示一行上的地块能放牛和不能让放牛的状态，一行上的地块选与不选的状态，例如一行上有4列，数字5(0101)，就代表选择第二块和第四块，这样每一行的状态都由一个数字表示。

    对于本题，假设一共有n列，则该列的状态一共有(1<<n)种状态，在本题中，要保证选择的两块地不相邻，因此在进行DP过程中，当前行的可选状态，只与上一行的状态有关，要满足下面几个条件：

    • 对于当前行的状态j，首先j中不能出现两个地块相邻，即j的数位中不出现两个1相邻，可以通过(j&(j<<1))==0来判断，若为true，说明j满足条件，若为false，说明不满足条件
    • 如果用value[i]来表示第i行的地块的肥沃和贫瘠的情况，1表示可以放牛，0表示不可以放牛，则第i行到的可选状态还必须满足(value[i]|j)==value[j]，若为true，说明j中的1都是来自value[i]中的1，就是说j所选择的地块都是第i行中的可以放牛的肥沃地块
    • 上面两个条件要求当前行的状态要满足哪些条件，当状态j满足的当前行的状态后，要需要与前一行的状态不产生冲突，假设k是满足前一行的一个可选状态，则当前行的状态j需要保证(j&k)==0，才能保证当前行与前一行中不存在上下相邻的行，对于当前行的状态j的方案数，就是所有满足上一行的可选状态且不与j产生冲突的状态方案数的总和

    在具体代码中，我们用value[]来保存每一行的可以放牛和不可以放牛的状态，用useful[]来保存所有自身不存在冲突的可选状态，即满足j&(j<<1))==0,用dp[i] [j]来表示第i行，状态j的方案数，最后总的方案数就是dp[n] [k]的总和，k为其中的一个状态，具体代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    #include <cstdio>
    #include <iostream>
    using namespace std;
    int value[13];//保存读入的每一行的01状态
    int useful[2000];//保存所有自身不冲突的状态
    int dp[13][2000];//i行j状态的方案数
    int main(){
      int m,n,t;
      scanf("%d%d",&m,&n);
      for(int i = 1;i<=m;i++){
      	for(int j = 0;j<n;j++){
        	scanf("%d",&t);
          	value[i]=(value[i]<<1)|t;
        }
      }
      int allstates = (1<<n)-1;
      int usefulstates=0;
      for(int i = 0;i<=allstates;i++){ //这里是进行一个预处理，现将所有自身不冲突的状态保存下来
      	if((i&(i<<1))==0){
        	useful[usefulstates++] = i;//将所有本身不冲突的状态保留
        }
      }
      for(int i = 0;i<usefulstates;i++){ //初始化第一行的状态
      	if((value[1]|useful[i])==value[1]){  //说明useful[i]的状态可以在第一行出现
        	dp[1][useful[i]] = 1;  //初始化第一行
        }
      }
      for(int i = 2;i<=m;i++){
      	for(int j = 0;j<usefulstates;j++){
        	if((value[i]|useful[j])==value[i]){  //对于本身不冲突的状态，判断其是否是当前行的可选状态，满足限制条件2
            	for(int k=0;k<usefulstates;k++){
                	if((useful[j]&useful[k])==0&&(useful[k]|value[i-1])==value[i-1]){ //判断与前一行是否存在冲突
                    	dp[i][useful[j]] += dp[i-1][useful[k]];  //前一行的状态k，也要满足前一行的可选条件
                      	dp[i][useful[j]] %=100000000;
                    }
                }
            }
        }
      }
      int ans = 0;
      for(int i = 0;i<usefulstates;i++){
      		ans+=dp[m][useful[i]];
         ans %=100000000;  //将所有状态的方案数求和
        }
      printf("%d\n",ans);
    }

2021-11-22

又摸了一天。。。

  • 剑指offer25.合并两个排序的链表

    easy遍历

  • 剑指offer26.树的子结构

    剑指26

先深度优先遍历找到头结点的值在A树中的位置，然后递归check下面的子树，注意终止条件即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    TreeNode d;
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        d= B;
        if(A==null&&B!=null) return false;
        if(A!=null&&B==null) return false;
        if(A==null&&B==null) return false;
        return find(A,B.val);
    }
    public boolean find(TreeNode r,int k){
        if(r==null) return false;
        if(r.val==k) {
            boolean ans = check(r,d);
            if(ans==true) return true;
        }
      return find(r.left,k) || find(r.right,k);
    }
    public boolean check(TreeNode r,TreeNode x){
        if(r==null&&x==null) return true;
        if(r!=null&&x==null) return true;
        if(r!=null&&x!=null){
            if(r.val == x.val)
            {
                return check(r.left,x.left)&&check(r.right,x.right);
            }
        }
        return false;
    }
}

  • 剑指offer28.对称的二叉树

    easy，递归判断即可

2021-11-20

学院csp线上测验，未得到完整题解，暂不记录

2021-11-18

  • 剑指offer14-1.剪绳子1

  • 剑指offer14-2.剪绳子2

    数学证明：每次切都切长度3

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    class Solution {
        public int cuttingRope(int n) {
            if(n<=3) return n-1;
            if(n==4) return 4;
            long res = 1;
            long mod =(long)1e9+7;
            while(n>4){
                res = (res*3)%mod;
                n = n-3;
            }
            return (int)((res*n)%mod);
            
            }
    }//主要是大数溢出，res和mod都要为long才行

    动态规划（后续补充）

  • 剑指offer 21.调整数组顺序使奇数位于偶数前面

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    class Solution {  //原地交换
        public int[] exchange(int[] nums) {
            int  i = 0;
            int tem=0;
            int j = nums.length-1;
            while(i<j){
                if((nums[i]&1)==0&&(nums[j]&1)==1){
                    tem = nums[i];
                    nums[i] = nums[j];
                    nums[j] = tem;
                    i++;
                    j--;
                }else if((nums[i]&1)==0&&(nums[j]&1)==0){
                    j--;
                }else if((nums[i]&1)==1&&(nums[j]&1)==1){
                    i++;
                }else{
                    i++;j--;
                }
            }
            return nums;
        }
    }

2021-11-16

  • 剑指offer 27.二叉树的镜像

    easy，递归处理

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    /**
     * Definition for a binary tree node.
     * public class TreeNode {
     *     int val;
     *     TreeNode left;
     *     TreeNode right;
     *     TreeNode(int x) { val = x; }
     * }
     */
    class Solution {
        public TreeNode mirrorTree(TreeNode root) {
            if(root == null) return null;
            return reverse(root);
        }
        public TreeNode reverse(TreeNode root){
            if(root == null) return null;
            TreeNode l = root.left;
            TreeNode r = root.right;
            root.left = reverse(r);
            root.right = reverse(l);
            return root;
        }
    }

  • 剑指offer 11.旋转数组的最小数字

    easy,初始最小设为数组第一个(考虑没有发生旋转的情况)，接着从左往右遍历，当发现下一个比当前的值小，说明下一个是旋转前的头一个，是最小的

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    class Solution {
        public int minArray(int[] numbers) {
            int len = numbers.length;
            int ans = numbers[0];
            for(int i = 0;i<len-1;i++){
                if(numbers[i]>numbers[i+1]){
                    ans = numbers[i+1];
                    break;
                }
            }
            return ans;

        }
    }

  • 剑指offer 12.矩阵中的路径

    剑指12

整体思路：DFS+标记位，自己做的时候有大概的思路，但是还是混乱的，在情况分类，边界条件上做了很多无用功，引以为戒。

DFS的递归思路：

递归变量：当前值在矩阵中的坐标i,j以及当前判断的目标字符串中的字符在数组中的位置

递归函数：

  1. 首先判断当前的坐标值，是否在正常的坐标范围内，如果不在，返回false，如果在，进一步判断
  2. 若当前坐标(i,j)出的字符与目标字符相同，且当前坐标未被使用过，flag[i] [j]为false，进一步处理。若不满足要求，说明找不到目标字符，返回false。
  3. 当判断当前位置找到了目标字符时，先将当前位置的标记设为true，即flag[i] [j]为true，接着递归判断当前位置的上下左右四个位置，只要有一个满足情况就说明找到了目标字符串，返回true，否则，说明此路不通，需要将当前位置的标记重新改为false，返回false，只有能走通的路才能被标记位true
  4. 如果当前坐标的字符与目标字符相同，且当前坐标未被访问，目标字符在数组中正好是最后一个，说明已经找到了所有的字符，直接返回true

初始代码：（极其混乱，注释部分过多代码冗余）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
    char[] c;
    char[][] tem;
    boolean[][] flag1;
    int length;
    int M=0,N=0;
    public boolean exist(char[][] board, String word) {
        c = word.toCharArray();
        length = c.length;
        tem = board;
        int m = board.length; //hang
        int n = board[0].length; //lies
        M = m;
        N = n; 
        boolean[][] flag = new boolean[m][n];
        boolean ans = false;
        flag1 = flag;
        if(m*n<length) return false;
        for(int i = 0;i<m;i++){
            for(int j =0;j<n;j++){
                if(tem[i][j]==c[0]){
                     ans = find(i,j,0);
                     if(ans == true)  return ans;
                    //  for(int a = 0;a<m;a++){//因为在递归函数里若当前路径没有找到，就会取消标记，因此不用再将所有的标记清除，这会做很多无用功，浪费很多时间
                    //      for(int b = 0;b<n;b++){
                    //          flag1[a][b] = false;
                    //      }
                    //  }
                }
            }
        }
        return false;
    }
    public boolean find(int i,int j,int x){
        boolean ans =false;
        if(i>=0&&i<M&&j>=0&&j<N){
            if(tem[i][j]==c[x]&&flag1[i][j]==false){
                flag1[i][j] = true;
                if(x==length-1) return true;
                // if(i==0&&j==0){
                //     ans = find(i+1,j,x+1)||find(i,j+1,x+1);
                //     if(ans == true) return true;
                //     flag1[i][j] = false;
                //    // return false;
                //  }
                // if(i==0&&j!=0){  //因为在一开始会判断坐标是否处于正常的范围，因此不需要在针对坐标做分类处理了，统一去找上下所有即可
                //   ans = find(i,j-1,x+1)||find(i,j+1,x+1)||find(i+1,j,x+1);
                //   if(ans == true) return true;
                //   flag1[i][j] = false;
                //   //return false;
                // }
                // if(i!=0&&j==0){
                //    ans = find(i-1,j,x+1)||find(i+1,j,x+1)||find(i,j+1,x+1);
                //    if(ans == true) return true;
                //     flag1[i][j] = false;
                //     //return false;
                // }
                // if(i!=0&&j!=0){
                ans =  find(i-1,j,x+1)||find(i+1,j,x+1)||find(i,j+1,x+1)||find(i,j-1,x+1);
                if(ans == true) return true;
                flag1[i][j] = false;
                //return false;
                }
            }
            return false;
        }
 }

最终版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    char[] c;
    char[][] tem;
    boolean[][] flag1;
    int length;
    int M=0,N=0;
    public boolean exist(char[][] board, String word) {
        c = word.toCharArray();
        length = c.length;
        tem = board;
        int m = board.length; //hang
        int n = board[0].length; //lies
        M = m;
        N = n; //保存一些全局变量，包括矩阵的行数和列数，目标字符串数组，标记矩阵等等
        boolean[][] flag = new boolean[m][n];
        boolean ans = false;
        flag1 = flag;
        if(m*n<length) return false;
        for(int i = 0;i<m;i++){
            for(int j =0;j<n;j++){
                if(tem[i][j]==c[0]){  //刚开始找第一个字符的时候，应该尝试对所有与目标字符串第一个字符相等的坐标
                     ans = find(i,j,0);
                     if(ans == true)  return ans;
                }
            }
        }
        return false;
    }
    public boolean find(int i,int j,int x){
        boolean ans =false;
        if(i>=0&&i<M&&j>=0&&j<N){
            if(tem[i][j]==c[x]&&flag1[i][j]==false){
                flag1[i][j] = true;
                if(x==length-1) return true;
                ans =  find(i-1,j,x+1)||find(i+1,j,x+1)||find(i,j+1,x+1)||find(i,j-1,x+1);
                if(ans == true) return true;
                flag1[i][j] = false;
            }
        }
        return false;
   }
 }

2021-11-15

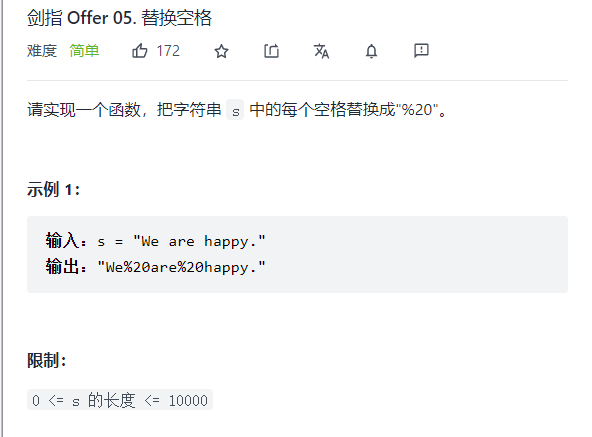
  • 剑指offer 05.替换空格 very easy

剑指05

对于java的string类型，它具有不可变型，使用StringBuilder类型保存结果，遍历s的每个 字符，当遇到空格使，向StringBuilder中加入“%20”，其他情况，加入当前字符。

主要是好久不做，相关API忘记了。。。

这里需要复习一下String，StringBuilder，和Stringbuffer的异同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public String replaceSpace(String s) {
            StringBuilder  ans = new StringBuilder();
            for(char c:s.toCharArray())
            {
                if(c==' '){
                    ans.append("%20");
                }else{
                    ans.append(c);
                }
            } 
            return ans.toString();
    }
}

  • 剑指offer 07.重建二叉树

    剑指07

关于本题的关键点：

  1. 前序遍历第一个就是根节点，中序遍历的根节点左边就是左子树，右边就是右子树
  2. 前序遍历的结构是[根节点，左子树，右子树]，且左子树和右子树部分的第一个分别是他们的根节点
  3. 中序遍历的结构是[左子树，根节点，右子树]
  4. 所以可以根据这样的结构去递归处理左子树和右子树

难点主要在于递归的结构，在递归过程中需要传递的变量值，这里使用一个HashMap来存储中序遍历中每个节点值和它在中序遍历的数组中的位置，这样可以在O(1)的条件下获取一个值在中序遍历中的索引。

递归算法分析：

  • 递归参数：

    root_pre_id：表示根节点在前序遍历中的索引，根据这个id可以获得当前树根节点的值，再根据根节点的值，可以在map中得到在根节点在中序遍历中的索引.

    in_left：当前树在中序遍历中的左边界

    in_right：当前树在中序遍历中的右边界

    根据上述三个参树，每次递归都可以计算出左节点或右节点在前序遍历中的索引，以及左右子树各自的左右边界。

  • 终止条件：in_left>in_right，说明已将越过了叶子结点，返回null

  • 每一次递归：

    1. 计算根据root_pre_id，得到根节点的值，建立根节点

    2. 根据根节点的值，得到根节点在中序遍历中的索引root_in_id

    3. 递归左右子树：

      递归变量：

      左子树：左子树根节点在前序遍历中的索引就是当前根节点在前序中的索引+1，即root_pre_id + 1,左子树在中序中的左边界就是当前的左边界，即in_left+1，右边界为当前根节点在中序中的索引-1，即root_in_id - 1

      右子树：右子树的根节点在前序遍历中的索引就是当前根节点在前序中的索引加上左子树的节点数量+1，即root_pre_id+(root_in_id - in_left) + 1，右子树的左边界为root_in_id +1，右边界为当前的右边界in_right

    4. 返回root

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int[] pre;
    private HashMap<Integer,Integer> id_index = new HashMap<Integer,Integer>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.pre = preorder;
        for(int i = 0;i<inorder.length;i++){
            id_index.put(inorder[i],i);  //使用map保存中序数组中的值与索引，避免每一次都遍历
        }
        return build(0,0,inorder.length-1);
    }
    public TreeNode build(int root_pre_id,int in_left,int in_right){
        if(in_left > in_right){  //终止条件
            return null;
        }
        TreeNode root = new TreeNode();  //创建当前的根节点
        root.val = pre[root_pre_id]; //获取根节点的值
        int root_in_id = id_index.get(root.val);  //获取根节点在中序中的索引
        root.left = build(root_pre_id+1,  in_left,  root_in_id-1); //递归左右子树(根节点的前序索引，中序左边界，中序右边界)
        root.right = build(root_pre_id+(root_in_id-in_left)+1,  root_in_id+1,  in_right);
        return root;       //根节点前序索引+左子树节点数+1
    }
}

  • 剑指offer 09 用两个栈实现队列

    思路：先用第一个栈保存数据，从队列尾部添加数据，就是把数据push到第一个栈中，当需要从队列头部取出数据时，现将第一个栈中的数据全部pop到第二个栈中，这样第二个栈的栈顶，就是队列头部的元素，pop出栈顶，再把剩下的元素在pop+push导到第一个站里面

  • 剑指offer 10 青蛙跳台阶

    简单DP