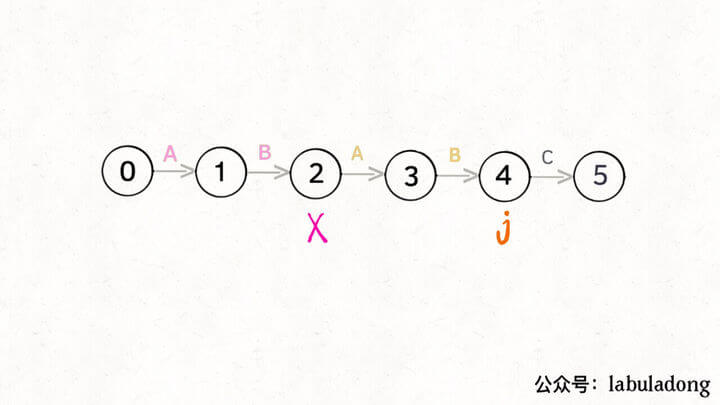KMP算法

KMP算法解析

KMP算法主要用于在一个字符串中找到另一个字符串，应用场景很多，但核心问题都是如何在一个文本字符串中，找到一个目标字符串。

主要有两种形式的KMP算法，一种是基于前缀表的解法，一种是基于有限状态机的解法。

基于前缀表的解法

主要参考《代码随想录》中的解题思想。

该方法主要利用一个叫next的前缀表的数组来判断：如果当前位置的字符不匹配时，根据之前已经匹配过的文本内容，需要退回到目标串的哪里开始再次匹配，而不是重头匹配。

前缀表的任务是：当前位置匹配失败后，找到之前已经匹配的位置再重新匹配，这也意味着在某个字符匹配失败后，前缀表会告诉你下一步匹配时目标串应该跳到哪个位置。

前缀表的定义为：记录下标i(包括i)之前的字符串中有多长的相同前后缀。

前缀：字符串中不包含最后一个字符的所有以第一个字符开头的连续子字符串。

后缀：字符串中不包含第一个字符的所有以最后一个字符结尾的连续子字符串。

字符串：a，最长相同前后缀的长度的0
字符串：aa，最长相同前后缀的长度为1，最长前缀：a，最长后缀：a
字符串：aab，最长相同前后缀的长度为0，因为最短前缀a，最短后缀b，不相同
字符串：aaba，最长相同前后缀的长度为1，最长前缀：a，最长后缀：a
字符串：aabaa，最长相同前后缀的长度为2，最长前缀：aa，最长后缀：aa
字符串：aabaaf，最长相同前后缀的长度为0，因为最短前缀a，最短后缀f，不相同

根据上面的分析，对于字符串aabaaf，他的前缀表为[0,1,0,1,2,0]。

构造next数组

• 初始化next数组
• 处理前后缀不相同的情况
• 处理前后缀相同的情况

next数组是目标串的前缀表，只根据目标串来构造，与文本串无关。

/*
使用i，j两个指针，i指向后缀的起始位置，j指向前缀的起始位置
初始化j = 0，next[0] = 0;
然后i从1开始，依次处理长度为2的字符串最长相同前后缀长度next[i]，即next[1],之后依次处理长度为2,3,4...的目标船的子字符串的最长相同前后缀长度。
如果当前前后缀相同，则j++，令next[i] = j，因为j是从0开始的，所以记录长度需要先++，之后下一轮循环，判断前后缀各自的下一个字符是否相同。
如果当前前后缀不同，就需要对j进行回退，获取当前比较的前缀字符j的前一个字符的next值，令j = next[j-1],然后继续比较i和j处的字符，这里是最巧妙的地方！！！很妙！！！我也不知道怎么解释😭😭
*/  
int[] next;
public void getNext(String s){
        int len = s.length();
        next = new int[len];
        next[0] = 0;
        int j = 0;
        for(int i = 1;i<len;i++){
            while(j>0&&s.charAt(j)!=s.charAt(i)){
                j = next[j-1];
            }
            if(s.charAt(i)==s.charAt(j)){
                j++;
            }
            next[i] = j;//next[i]是当前位置的字符串的最长相同前后缀的长度，因为是长度所以先++之后赋的值。
        }
    }

得到next数组之后,我们便可以根据next数组去进行字符串匹配。

/*
首先获取next数组，接下来开始进行匹配
i指向文本串当前所需要匹配的字符，j指向目标串当前所需要匹配的字符
整个匹配过程中，i一直向前推进，只有目标串根据匹配情况不断调整下一次匹配的位置
*/
		getNext(needle);//获取next数组（前缀数组）
        int len = needle.length();
        int j = 0;
        for(int i = 0;i < haystack.length();i++){
            while(j>0&&haystack.charAt(i)!=needle.charAt(j)){
                j = next[j-1];//当前不匹配时，根据当前元素的前一个元素的next值去直到，当前的i应该继续和匹配串中的哪一个去匹配。
            }
            if(haystack.charAt(i)==needle.charAt(j)){
                j++;//如果当前值匹配，则继续匹配下一个字符
            }
            if(len==j){
                return ;//匹配完成，找到了目标字符串
            }         
        }
	    return ;//匹配失败，没找到

对于字符串aabaaf，得到next数组为[0,1,0,1,2,0]
假设当前需要匹配第六个字符，如果文本串为aaaaabaabaaf，当前已匹配的情况为aaa aabaa baaf
当前需要匹配b和f是否相同，结果是不同，此时需要根据next数组去重新调整j的值，j当前为5，此时匹配不成功，根据经验，我们应该重新调整令j=2，即与目标字符串的第三个字符b来比较，因为当我们比较到j=5时，已经知道前面有aa了，所以需要令j等于2，而2正是目标字符串的前缀表中，j当前字符的前一个字符的next值，因此令
j=next[j-i],下一步需要跳到的位置就是next[j-1],将此位置的字符与当前i位置的字符进行比较。

我直呼：”妙啊！”。虽然为什们这样做还是一知半解。

lc-28.实现strStr()

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

使用前缀表的解题代码：

class Solution {

    int[] next;

    public void getNext(String s){
        int len = s.length();
        next = new int[len];
        next[0] = 0;
        int j = 0;
        for(int i = 1;i<len;i++){
            while(j>0&&s.charAt(j)!=s.charAt(i)){
                j = next[j-1];
            }
            if(s.charAt(i)==s.charAt(j)){
                j++;
            }
            next[i] = j;//next[i]是当前位置的字符串的最长相同前后缀的长度，因为是长度所以先++之后赋的值。
        }
    }
    public int strStr(String haystack, String needle) {
        if(haystack == null) return -1;
        if(needle == null||needle.length()==0) return 0;
        getNext(needle);//获取next数组（前缀数组）
        int len = needle.length();
        int j = 0;
        for(int i = 0;i < haystack.length();i++){
            while(j>0&&haystack.charAt(i)!=needle.charAt(j)){
                j = next[j-1];//当前不匹配时，根据当前元素的前一个元素的next值去直到，当前的i应该继续和匹配串中的哪一个去匹配。
            }
            if(haystack.charAt(i)==needle.charAt(j)){
                j++;//如果当前值匹配，则继续匹配下一个字符
            }
            if(len==j){
                return i - len + 1;
            }      
        }
        return -1;
    }
}

基于有限状态机的解法

主要参考labuladong的算法详解，KMP 算法详解

解题思想主要是将模式串的匹配转换为有限状态机的状态转换，当前状态接收某个字符，然后转到对应的下一个状态，如果进入到最终状态，说明完成了目标串的识别，即完成了匹配。

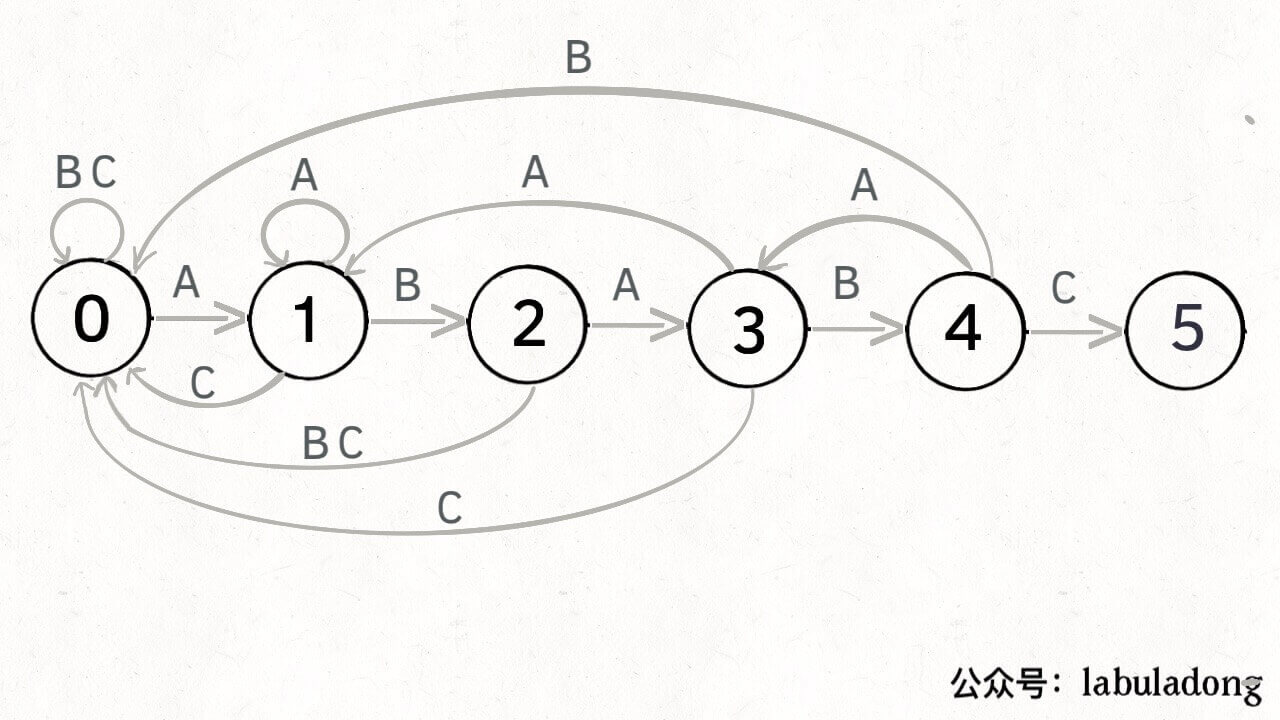
例如，识别目标串ABABC，其对应的有限状态机的转换为：

根据状态机，当我们确定两个变量：(当前的匹配状态和遇到的字符)，我们就知道在这个情况下应该转移到那个状态。

我们使用二维dp数组来描述这个状态转移图：

dp[j][c] = next
0 <= j < M，代表当前的状态
0 <= c < 256，代表遇到的字符（ASCII 码）
0 <= next <= M，代表下一个状态

dp[4]['A'] = 3 表示：
当前是状态 4，如果遇到字符 A，
pat 应该转移到状态 3

dp[1]['B'] = 2 表示：
当前是状态 1，如果遇到字符 B，
pat 应该转移到状态 2

根据这个dp数组，我们就可以写出目标串匹配的函数：

public int search(String txt) {
    int M = pat.length(); //目标串
    int N = txt.length(); //文本串
    // pat 的初始态为 0
    int j = 0;
    for (int i = 0; i < N; i++) {
        // 当前是状态 j，遇到字符 txt[i]，
        // pat 应该转移到哪个状态？
        j = dp[j][txt.charAt(i)];
        // 如果达到终止态，返回匹配开头的索引
        if (j == M) return i - M + 1;
    }
    // 没到达终止态，匹配失败
    return -1;
}

可以看出，解决问题的核心在于如何根据目标串，得到对应有限状态机的状态转移图。

定义一个dp数组：

for 0 <= j < M: # 状态
    for 0 <= c < 256: # 字符
        dp[j][c] = next

如何知道下一个状态next呢？如果遇到的字符c与pat[j]匹配，则状态应该向前推进，则此时next = j + 1。如果遇到的字符c与pat[j]不匹配呢？此时肯定应该回退到之前的某个状态，并且之前的某个状态已经完成的匹配部分与我们当前已经匹配的过的前面的字符相同。

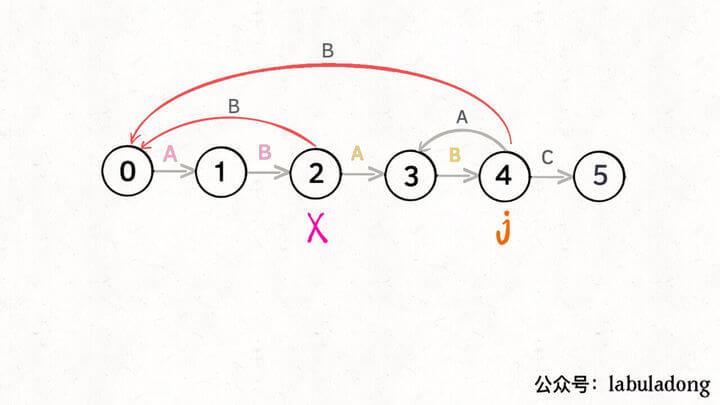
这里，我们使用一个叫做影子状态的变量X来表示，所谓影子状态，就是和当前状态具有相同的前缀，比如下面这种情况：

当前状态 j = 4，其影子状态为 X = 2，它们都有相同的前缀 “AB”。因为状态 X 和状态 j 存在相同的前缀，所以当状态 j 准备进行状态重启的时候（遇到的字符 c 和 pat[j] 不匹配），可以通过 X 的状态转移图来获得最近的重启位置。

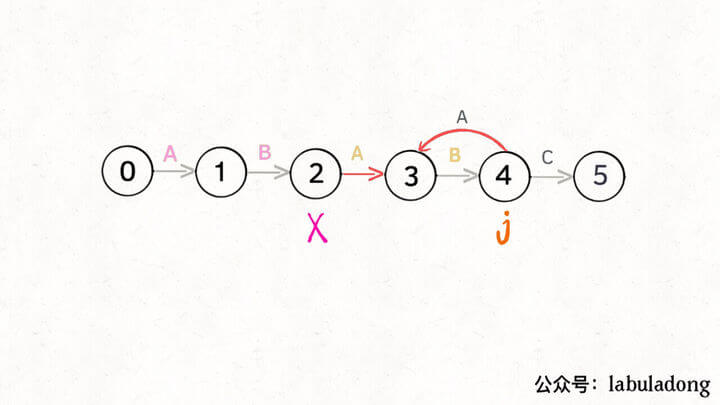
比如说刚才的情况，如果状态 j 遇到一个字符 “A”，应该转移到哪里呢？首先只有遇到 “C” 才能推进状态，遇到 “A” 显然只能进行状态重启。**状态 j 会把这个字符委托给状态 X 处理，也就是 dp[j]['A'] = dp[X]['A']**：

为什么这样可以呢？因为：既然 j 这边已经确定字符 “A” 无法推进状态，只能回退，而且 KMP 就是要尽可能少的回退，以免多余的计算。那么 j 就可以去问问和自己具有相同前缀的 X，如果 X 遇见 “A” 可以进行「状态推进」，那就转移过去，因为这样回退最少。

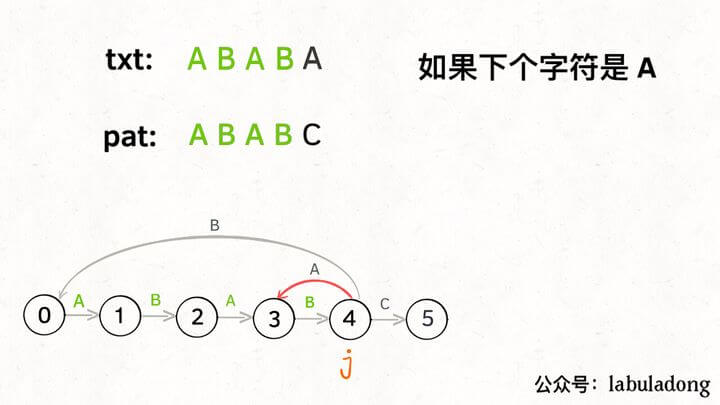
当然，如果遇到的字符是 “B”，状态 X 也不能进行「状态推进」，只能回退，j 只要跟着 X 指引的方向回退就行了：

你也许会问，这个 X 怎么知道遇到字符 “B” 要回退到状态 0 呢？因为 X 永远跟在 j 的身后，状态 X 如何转移，在之前就已经算出来了。动态规划算法不就是利用过去的结果解决现在的问题吗？

而关于影子变量X的更新，其实只需要根据j处接收的字符一同进行状态更新就行了，比如上面的j此时为4状态，j需要接收C前进，此时X也需要转到接收C的下一个状态，这样才能保证X始终与j具有相同的前缀，作为j的影子状态，因此有X = dp[X][pat[j]];。

最后可以得到构造dp二维数组的函数代码：

public void getDp(String s){
    int len = s.length();
    dp = new int[len][256];
    char[] c = s.toCharArray();
    dp[0][c[0]] = 1;
    int X = 0;//影子标记
    for(int i =1;i<len;i++){
        for(char cc = 0;cc<256;cc++){
            dp[i][cc] = dp[X][cc]; //将影子状态复制过来
        }
        dp[i][c[i]] = i+1;//更新当前正确匹配字符的下一状态为i+1
        X = dp[X][c[i]];//更新影子状态的下一状态
    }         
}

lc-28.实现strStr()

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

使用状态机的解题代码：

class Solution {

    int[][] dp;

    public void getDp(String s){
        int len = s.length();
        dp = new int[len][256];
        char[] c = s.toCharArray();
        dp[0][c[0]] = 1;
        int X = 0;//影子标记
        for(int i =1;i<len;i++){
            for(char cc = 0;cc<256;cc++){
                dp[i][cc] = dp[X][cc];
            }
            dp[i][c[i]] = i+1;
            X = dp[X][c[i]];
        }         
    }
    public int strStr(String haystack, String needle) {
        if(haystack == null) return -1;
        if(needle == null||needle.length()==0) return 0;
        getDp(needle);//获取next数组（前缀数组）
        int j = 0;
        char[] haystacks = haystack.toCharArray();
        char[] needles = needle.toCharArray();
        for(int i = 0;i<haystack.length();i++){
            j = dp[j][haystacks[i]];
            if(j==needles.length){
                return i -needles.length + 1;
            }
        }
        return -1;
     
    }
}